Lunar Crossing
Why the Moon crosses the meridian, on average, 50.5 minutes later each day
In one day the Earth rotates 360° and the Moon orbits around the Earth about 13.2°. An observer sees the Moon on the meridian at a specific time. We wish to determine when they will next see the Moon on the meridian.
For an initial estimate of this time interval we could calculate how long the Earth takes to rotate (360+13.2)°, i.e.
373.2/360×24 = 24.88 hours = 24h 52.8m.
Hence the observer would see the Moon cross the meridian about 52.8m later the next day. While this is a good initial estimate we can determine an accurate value as follows.
Let E be the Earth’s sidereal rotation period in hours and
M the Moon’s sidereal orbital period around the Earth in hours.
If the Moon crosses the meridian at a specific time, let t be the time interval to when the Moon next crosses the meridian. In this time interval the Earth has rotated t×360/E° and the Moon has orbited around the Earth t×360/M°. We wish to determine the time interval when the angle that the Earth has rotated, minus 360°, is equal to the angle the Moon has orbited the Earth. So
t*360/E - 360 = t*360/M
t/E - 1 = t/M
1/E - 1/t = 1/M
1/E - 1/M = 1/t
t = 1 /( 1/E - 1/M )
Now E = 23.93447 hours (i.e. 23h 56m 4.0989s) and M = 655.7180 hours (i.e. 27.321582d × 24), so substituting in the above equation, we find
t = 24.84120 hours = 24h 50.5m.
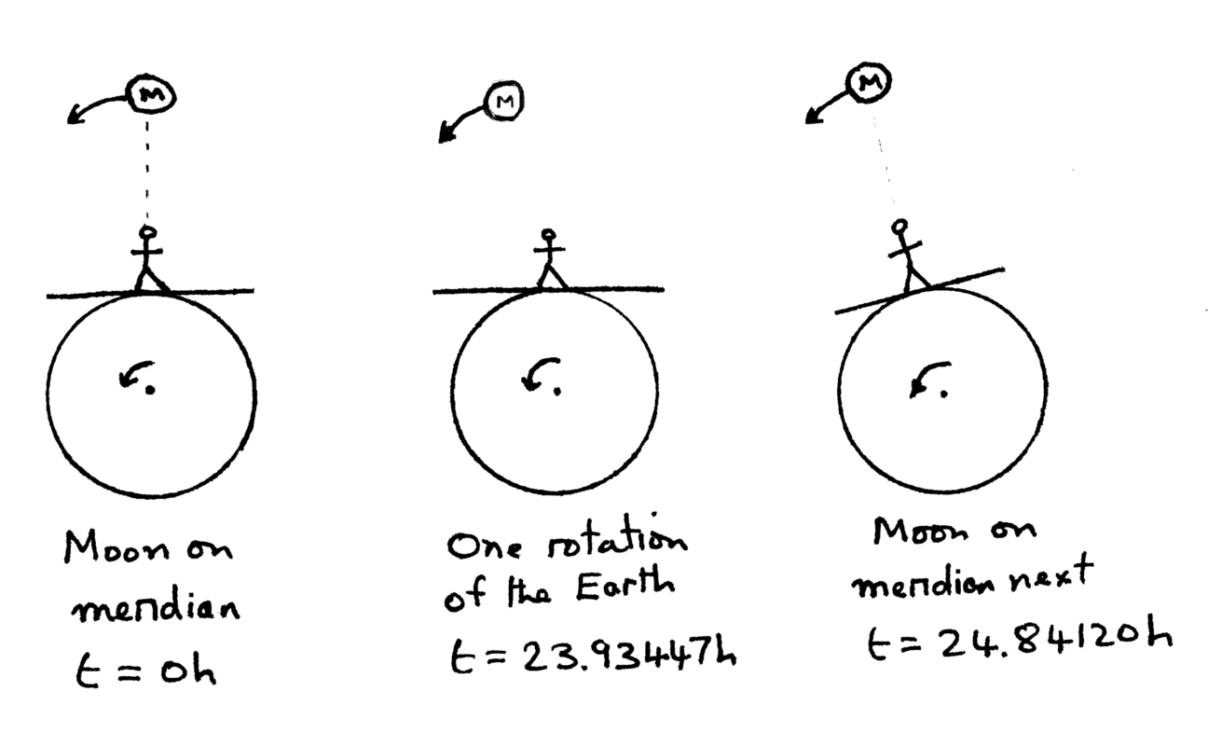
Hence the Moon crosses the meridian, on average, 50.5m later each day. This also applies to the Moon rise and set times.
Tides on the Earth are primarily caused by the gravitational pull of the Moon. The period between successive high tides is 12h 25m, i.e. half the time of meridian lunar transits.Tides FAQ at NOC
See also Richard Pogge’s Lecture 20: Tides.
