Solar and Sidereal Days
In 24 hours the Earth rotates ~361° and the Earth revolves ~1° around the Sun.
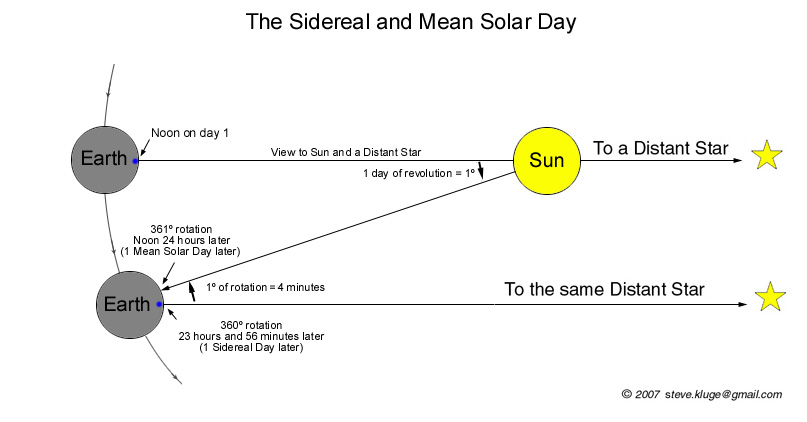
Let PSID be the sidereal rotation period of the Earth (i.e. the sidereal day = 23.93445 h),
PSOLAR be the length of the solar day (i.e. 24 h) and
PYEAR be the length of the year (i.e. 365.256 d).
The angular rotation speed of the Earth is 360/PSID [in ° per hour if PSID is in hours].
The angular revolution speed of the Earth around the Sun is 360/PYEAR [ in ° per day if PYEAR is in days]
In the time period PSOLAR the Earth rotates (360/PSID) × PSOLAR°
and the Earth revolves around the Sun (360/PYEAR) × PSOLAR°.
Now removing the complete turn of the Earth, i.e. 360°, we have
(360/PSID) × PSOLAR − 360° = (360/PYEAR) × PSOLAR
so 1/PSID − 1/PSOLAR = 1/PYEAR
or 1/PSID = 1/PSOLAR + 1/PYEAR
Hence if PSOLAR is 24 h and PYEAR is 365.256 × 24 h,
then PSID is 23.93445 h ( = 23h 56m 04s).
