Local Sidereal Time
Local Sidereal Time
Solar time is measured with respect to the position of the Sun. Our civil clocks, to a first approximation, are based on solar time and are designed such that when the Sun crosses the observer’s meridian the time is about noon, i.e. 12:00. (The world is divided into time zones so that at each location this is approximately true.). Of course, the apparent motion of the Sun across the sky is actually caused by the rotation of the Earth. So our clocks measure the length of time required for the Earth to rotate once with respect to the Sun. From our perspective, the Sun revolves around the Earth every 24 hours. This period is known as a solar day and is defined as the average length of time that the Sun takes to return to the same place in the sky, e.g. the observer’s meridian. (The length of a solar day actually varies during the year by a small amount due to the elliptical nature of the Earth’s orbit and the Earth’s 23.5° axial tilt relative to the ecliptic, see Equation of time)
Over the course of one day the Earth moves about 1° along its orbit around the Sun (360° divided by 365.25 days is about 1°). Therefore in one solar day the Earth has to spin 360° plus 1° to make the Sun return to the same position in the sky. So the actual period of rotation of the Earth relative to the distant stars, i.e. the time for the Earth to spin 360°, is less than one solar day.
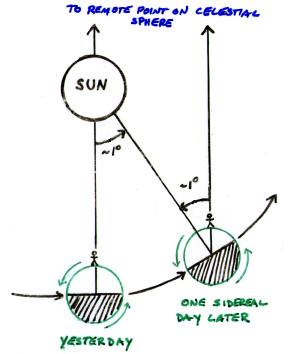
The time period for Earth to rotate 360°, relative to the distant stars, is called the sidereal day and is 23h 56m 04s of a solar day. This is about 4 minutes less than the solar day. The sidereal day is divided into 24 sidereal hours. Each sidereal hour is divided into 60 sidereal minutes and each sidereal minute is divided into 60 sidereal seconds.
A sidereal clock is designed to complete 24 hours of sidereal time in 23h 56m 04s of civil (solar) time. As such a clock runs at the same rate as the Earth’s rotation it can be used directly to specify precisely how much the Earth has rotated. For example, if we see the sidereal clock change by 6h we know immediately that the Earth has rotated by 90°, i.e. 360° × 6/24.
We use the term local sidereal time to denoted the RA coordinate on the celestial sphere that currently lies on the observer’s meridian. Recall that the RA coordinate measures positions around the equator of the celestial sphere (i.e. equivalent to longitude on the Earth surface) and has units of time (hours, minutes, seconds). Now take a sidereal clock and adjust the time to read the RA coordinate that is currently crossing your meridian. This clock will now always display the RA coordinate that is on your meridian as it will precisely run at the Earth’s true rotation rate. Solocal sidereal time (LST)=the RA on the observer’s meridian
The local sidereal time is clearly very useful for astronomers. It can be calculated from the local civil time and observer’s longitude using a relatively simple formula, see e.g. Page 16-20, Duffett-Smith’s “Practical Astronomy” or Page 40-1, Montebruck and Pfleger’s “Astronomy on the Personal Computer (4th edition)”.
USNO’s online Sidereal Clock
